Lujuuslaskentaa viivottimella, harpilla ja ruutupaperilla
Lujuuslaskenta on yleensä ottaen melko haastava ala. Asialliseen, ammattimaiseen lujuuslaskentaan vaaditaan pitkä koulutus ja työssä oppiminen sekä kalliit ohjelmistot, vaikka tietokoneiden puolesta monet e-urheilijatkin käyttävät tehokkaampia laitteita kuin lujuuslaskennassa yleensä käytetään (toki erittäin suurissa laskentatöissä monenkymmenen koneen klustereitakin voidaan tarvita).
On kuitenkin syytä muistaa, että vielä esimerkiksi Apollo -ohjelman aikoihin 1960 -luvulla ihminen lennätettiin kuuhun ja takaisin käytännössä ilman tietokoneiden tarjoamaa apua rakenteiden lujuuden laskennassa. Normaalilla insinöörillä oli käytettävissään ehkä laskutikku ja mekaaninen laskin kynän, paperin, harpin, viivottimen ja splinin lisäksi. Laskenta perustui noihin aikoihin pitkälti perusstatiikkaan sekä palkki- laatta- ja kuoriteorian analyyttisiin käsikirjakaavoihin ja taulukkotapauksiin (esim Roark), joilla voitiin rakenteen lujuutta (ainakin teoriassa) arvioida joissain tapauksissa jopa FE-laskentaa tarkemminkin. Vielä nykyäänkin on esimerkiksi pintapaineiden laskenta usein järkevämpää laskea kaavoista kuin FE-analyysillä. Käytössä oli myös erilaisia graafisia menetelmiä.
Joskus jouduttiin kuitenkin ratkaisemaan suuriakin yhtälöryhmiä käsin esimerkiksi ristikoiden laskennassa, mikä on epäilemättä ollut äärimmäisen turhauttavaa ja häiriöherkkää työtä. Käytännössä laskennallisesti voitiinkin analysoida vain hyvin riisuttuja rakenteita yrittäen keskittyä vain oleellisiin asioihin hyvin suunnitellussa perusrakenteessa. Tulokseksi saatiin mitoitus, jonka toimivuus jouduttiin testaamaan nykylaskennalla saatavia mitoituksia useammin.
Nykyäänkin on lujuuslaskijan tai suunnittelijankin syytä hallita käsin mitoitus edes statiikan perussääntöjen mukaan. Ne ovat korvaamattomia esimerkiksi laskennan oikeellisuuden karkeassa tarkistamisessa ja toisinaan niillä saadaan suoraan laskettua rakenteen ja tukipisteiden kuormatkin suoraan helposti ja nopeasti. Statiikan hyvä hallinta auttaa myös erittäin paljon järkevien rakenteiden perusratkaisujen luomisessa kuormien tehokkaan kulkeutumisen kuormituspisteistä tukiin ollessa huomioitu.
Esimerkiksi allaolevasta tapauksesta, jossa kolmiokehällä kannatetaan kuormaa F, pitäisi jokaisen suunnittelijankin pystyä ratkaisemaan ainakin tukivoimat a:ssa ja b:ssä sekä sauvavoimat A,B ja C, tarvittaessa vaikka pelkän ruutupaperin paperin, kynän ja viivottimen avulla melko tarkastikin. Tuki a estää vain vaakasuuntaiset siirtymät ja pisteessä b on kiinnitetty sekä vaaka- että pystysuuntaiset siirtymät. Ratkaisu on alempana, mutta harjoituksen vuoksi voisi olla hyvä itse kunkin välillä testata omallakin kohdallaan tarvitsisiko statiikan perussääntöjä ehkä hieman kerrata. Vinkkinä F-vektori kannattaa piirtää johonkin tasamittaan, esimerkin tapauksessa vaikkapa 10mm pituiseksi, jolloin muitakin vektoreita on helpompi piirtää oikean pituisiksi.
Pystyreaktio b:ssä on luonnollisesti F ylös, koska se on ainoa piste jossa on tuki kuorman suunnassa.
Mittaamalla viivottimella saadaan b:n ja F:n välille varreksi 20mm, mikä aiheuttaa momenttia F:n ja b:n voimaparin vuoksi. Tämän momentin kantaa vaakasuuntainen tukivoimapari a:n ja b:n välillä, joiden väliseksi matkaksi saadaan 30mm. Koska momentit ja vaakavoimat on oltava tasapainossa, saadaan vaakatukivoimaksi a:ssa 20/30 x F vasemmalle ja b:ssä 20/30 x F oikealle (ok, myönnetään, tässä vaiheessa pitäisi pystyä arvioimaan 2/3~0.67 F pituinen viiva vaikkapa laskimella -- tai kynällä ja paperilla!) Resultanttivoiman suuruuden b:ssä suhteessa F:ään voi tämän jälkeen mitata viivottimella muodostamalla resultantin alakuvan, että resultanttivoima b:ssä on noin 1.2F yläviistoon.
Kannattaa muuten huomata, että tässä voi käyttää myös hyväkseen samanmuotoisia kolmioita kehän ja b-resultanttikuvion kesken, ja saada resultanttivoima suhteessa F:ään suoraan vinosauvan ja pystysauvan mitattujen pituuksien suhteesta (36mm / 30mm = 1.2)!
Sauvavoima A:ssa on luonnollisesti F (puristusta) ja B:ssä 2/3F (puristusta) suoraan b:ssä vallitsevista tukireaktioista A:n ja B:n ollessa suorassa kulmassa ja voimakomponenttien suuntaisia. Vastaavasti sauvavoima C:ssä saadaan vaikkapa a:ssa vallitsevasta voimien tasapainoehdosta, voiman A.ssa ollessa 1F ylöspäin ja tukireaktion a:ssa ollessa vasemmalle 2/3F, joista saadaan resultantiksi myös C-sauvalle sama arvo kuin edellä b:n voimaresultantiksi (=1.2F) vetoa.
"Kotitehtävä"
Mohrin ympyrällä voi myös helposti selvittää jännityskomponentit mielivaltaisessa suunnassa kiertämällä edellisessä kuvassa sinisellä esitettyä viivaa 2x suuntakulman verran haluttuun suuntaan. sx' ja sy' saadaan projisoimalla saadun viivan ja ympyrän leikkauspisteet vaaka-akselille ja leikkausjännitys txy' projisoimalla toinen niistä pystyakselille.
On kuitenkin syytä muistaa, että vielä esimerkiksi Apollo -ohjelman aikoihin 1960 -luvulla ihminen lennätettiin kuuhun ja takaisin käytännössä ilman tietokoneiden tarjoamaa apua rakenteiden lujuuden laskennassa. Normaalilla insinöörillä oli käytettävissään ehkä laskutikku ja mekaaninen laskin kynän, paperin, harpin, viivottimen ja splinin lisäksi. Laskenta perustui noihin aikoihin pitkälti perusstatiikkaan sekä palkki- laatta- ja kuoriteorian analyyttisiin käsikirjakaavoihin ja taulukkotapauksiin (esim Roark), joilla voitiin rakenteen lujuutta (ainakin teoriassa) arvioida joissain tapauksissa jopa FE-laskentaa tarkemminkin. Vielä nykyäänkin on esimerkiksi pintapaineiden laskenta usein järkevämpää laskea kaavoista kuin FE-analyysillä. Käytössä oli myös erilaisia graafisia menetelmiä.
Joskus jouduttiin kuitenkin ratkaisemaan suuriakin yhtälöryhmiä käsin esimerkiksi ristikoiden laskennassa, mikä on epäilemättä ollut äärimmäisen turhauttavaa ja häiriöherkkää työtä. Käytännössä laskennallisesti voitiinkin analysoida vain hyvin riisuttuja rakenteita yrittäen keskittyä vain oleellisiin asioihin hyvin suunnitellussa perusrakenteessa. Tulokseksi saatiin mitoitus, jonka toimivuus jouduttiin testaamaan nykylaskennalla saatavia mitoituksia useammin.
Nykyäänkin on lujuuslaskijan tai suunnittelijankin syytä hallita käsin mitoitus edes statiikan perussääntöjen mukaan. Ne ovat korvaamattomia esimerkiksi laskennan oikeellisuuden karkeassa tarkistamisessa ja toisinaan niillä saadaan suoraan laskettua rakenteen ja tukipisteiden kuormatkin suoraan helposti ja nopeasti. Statiikan hyvä hallinta auttaa myös erittäin paljon järkevien rakenteiden perusratkaisujen luomisessa kuormien tehokkaan kulkeutumisen kuormituspisteistä tukiin ollessa huomioitu.
Esimerkiksi allaolevasta tapauksesta, jossa kolmiokehällä kannatetaan kuormaa F, pitäisi jokaisen suunnittelijankin pystyä ratkaisemaan ainakin tukivoimat a:ssa ja b:ssä sekä sauvavoimat A,B ja C, tarvittaessa vaikka pelkän ruutupaperin paperin, kynän ja viivottimen avulla melko tarkastikin. Tuki a estää vain vaakasuuntaiset siirtymät ja pisteessä b on kiinnitetty sekä vaaka- että pystysuuntaiset siirtymät. Ratkaisu on alempana, mutta harjoituksen vuoksi voisi olla hyvä itse kunkin välillä testata omallakin kohdallaan tarvitsisiko statiikan perussääntöjä ehkä hieman kerrata. Vinkkinä F-vektori kannattaa piirtää johonkin tasamittaan, esimerkin tapauksessa vaikkapa 10mm pituiseksi, jolloin muitakin vektoreita on helpompi piirtää oikean pituisiksi.
 |
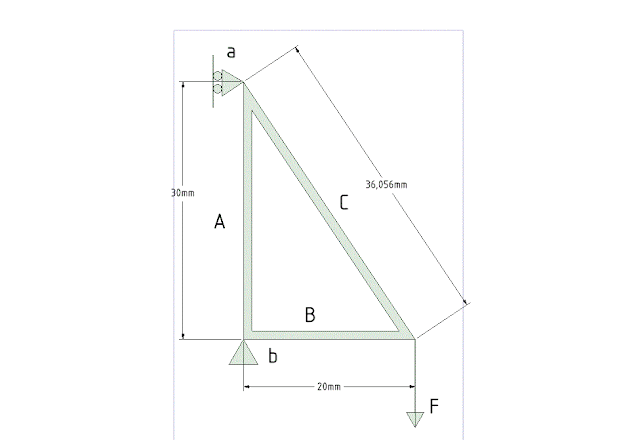| Esimerkkiongelma |
Ratkaisu
Voidaan todeta että rakenteen tuenta on "staattisesti määrätty", eli tässä tapauksessa tukia on yhtä monta (3) kuin tuntemattomia voimia tasossa ja laskenta voidaan suorittaa statiikan perusteiden avulla; Voimia ovat tasotapauksessa voima vaakaan ja pystyyn sekä momentti tason normaalin (=kuvatasosta poispäin) ympäri. Tukia puolestaan ovat vaakatuki a:ssa ja b:ssä sekä pystytuki b:ssä. Tällöin voidaan suoraan ratkaista tuntemattomat tukireaktiot suoraan tuntematta rakenteen jäykkyyttä:Pystyreaktio b:ssä on luonnollisesti F ylös, koska se on ainoa piste jossa on tuki kuorman suunnassa.
Mittaamalla viivottimella saadaan b:n ja F:n välille varreksi 20mm, mikä aiheuttaa momenttia F:n ja b:n voimaparin vuoksi. Tämän momentin kantaa vaakasuuntainen tukivoimapari a:n ja b:n välillä, joiden väliseksi matkaksi saadaan 30mm. Koska momentit ja vaakavoimat on oltava tasapainossa, saadaan vaakatukivoimaksi a:ssa 20/30 x F vasemmalle ja b:ssä 20/30 x F oikealle (ok, myönnetään, tässä vaiheessa pitäisi pystyä arvioimaan 2/3~0.67 F pituinen viiva vaikkapa laskimella -- tai kynällä ja paperilla!) Resultanttivoiman suuruuden b:ssä suhteessa F:ään voi tämän jälkeen mitata viivottimella muodostamalla resultantin alakuvan, että resultanttivoima b:ssä on noin 1.2F yläviistoon.
Kannattaa muuten huomata, että tässä voi käyttää myös hyväkseen samanmuotoisia kolmioita kehän ja b-resultanttikuvion kesken, ja saada resultanttivoima suhteessa F:ään suoraan vinosauvan ja pystysauvan mitattujen pituuksien suhteesta (36mm / 30mm = 1.2)!
 |
| Tukireaktiot a:ssa ja b:ssä samassa mittakaavassa F:n kanssa |
Sauvavoima A:ssa on luonnollisesti F (puristusta) ja B:ssä 2/3F (puristusta) suoraan b:ssä vallitsevista tukireaktioista A:n ja B:n ollessa suorassa kulmassa ja voimakomponenttien suuntaisia. Vastaavasti sauvavoima C:ssä saadaan vaikkapa a:ssa vallitsevasta voimien tasapainoehdosta, voiman A.ssa ollessa 1F ylöspäin ja tukireaktion a:ssa ollessa vasemmalle 2/3F, joista saadaan resultantiksi myös C-sauvalle sama arvo kuin edellä b:n voimaresultantiksi (=1.2F) vetoa.
Huomattakoon että suurempikin ristikko, jossa em. kolmio jatkuu vasemmalle ylä- ja alapaarteilla ja diagonaalisauvalla staattisesti määrättynä rakenteena (esimerkiksi nosturipalkki) voidaan laskea samalla menetelmällä. Saadun kolmion tukivoimat siirretään seuraavaan rakenneosaan vastakkaissuuntaisina voimina, josta ratkaistaan rakennevoimat tälle rakenneosalle. Tätä jatketaan kunnes päästään tukirakenteisiin.
Kotitehtävä: Laske edellisen perusteella allaolevan ulokeristikon sauvavoimat, kun yhden ristikkomodulin mitat ovat samat kuin edellä. Työtä voi helpottaa huomioimalla rakenteen toistuvuus ja taskulaskintakin saa käyttää 😉
"Kotitehtävä"
Mohrin ympyrät
Olin opintojeni alussa vuonna 1986 ensimmäisiä lujuusopin opiskelijoita, joille ei enää opetettu Mohrin ympyröiden käyttöä lujuuslaskennassa muuten kuin sivulauseessa. Mohrin ympyrät on graafinen menetelmä, jolla voi helposti selvittää pääjännitykset suuntineen sekä maksimileikkausjännitys yleiselle tasojännitystilalle millimetripaperilla, harpilla ja viivottimella. Tämä selittää myös osittain Trescan, ts. maksimileikkauskriteerin suosion vanhoissa, ennen laskimia ja tietokoneita tehdyissä määräyksissä tarkemman, mutta ilman laskimia hankalan von Misesin kriteerin sijaan. Laskimien yleistyttyä von Misesin kriteerin arvon laskeminen on tullut helpoksi ja Mohrin ympyrät ovat jääneet monen muun mielenkiintoisen ja aikanaan tärkeän menetelmän tapaan historialliseksi kuriositeetiksi.
Oletetaan että tasojännitystila jossain tasossa olevassa XY -koordinaatistossa on tunnettu, jossa sx on jännitys x-suuntaan, sy jännitys y-suunnassa ja txy leikkausjännitys. Piirretään vaakasuora viiva, jolle valitaan origo. Piirretään seuraavaksi pystyviiva, jonka etäisyys origosta on sx ja toinen pystyviiva, jonka etäisyys on sy (jos jännitys on puristusta, sen merkki on negatiivinen ja viiva piirretään origon vasemmalle puolelle), esimerkkikuvassa alla vihreät viivat. Piirretään seuraavaksi kaksi vaakaviivaa etäisyydelle txy origoviivasta, toinen origon yläpuolelle ja toinen alapuolelle (punaiset viivat). Piirretään tämän jälkeen viiva vinosti saatujen leikkausjännitysviivojen txy ja sx/sy risteysten väliin (kuvassa sininen viiva). Lopuksi piirretään harpilla ympyrä, jonka keskipiste on vinoviivan ja origon kautta kulkevan vaakaviivan risteyksessä ja jonka kehä kulkee txy/sx ja txy/sy -risteysten kautta.
Tuloksena saadaan luettua pääjännitykset tasossa origovaakaviivan ja ympyrän kahdesta risteyksistä. Maksimileikkausjännitys on ympyrän säde ja pääjännitysten kulmaksi koordinaatistoon saadaan lävistäjäviivan ja vaakaviivan välisen kulman puolikas. Pääjännitysten kulman etumerkki täytyy päätellä leikkausjännityksen etumerkistä.
Esimerkki alla, käyttäen paperin sijasta LibreCadia kuvion piirtämiseksi. Tässä tapauksessa tasojännitystilassa sx=100, sy=-40 ja txy=50 yksikköä. Mohrin ympyrä piirtämällä ja mittaamalla voi todeta maksimileikkausjännityksen olevan 86 yksikköä, maksimipääjännityksen 116 yksikköä ja minimipääjännityksen -56 yksikköä. Maksimipääjännityksen suuntakulma x-akselista on 36 / 2 = 18 astetta.
Esimerkki alla, käyttäen paperin sijasta LibreCadia kuvion piirtämiseksi. Tässä tapauksessa tasojännitystilassa sx=100, sy=-40 ja txy=50 yksikköä. Mohrin ympyrä piirtämällä ja mittaamalla voi todeta maksimileikkausjännityksen olevan 86 yksikköä, maksimipääjännityksen 116 yksikköä ja minimipääjännityksen -56 yksikköä. Maksimipääjännityksen suuntakulma x-akselista on 36 / 2 = 18 astetta.
 |
| Mohrin ympyrän laskentaesimerkki |
Kommentit
Lähetä kommentti